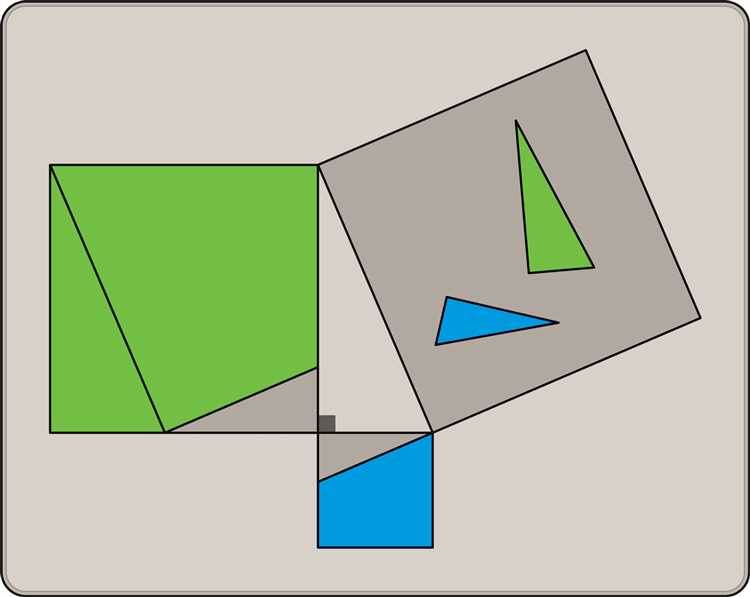
Геометрия — это одна из древнейших наук, которая волновала умы людей на протяжении веков. Множество головоломок и задач были разработаны для того, чтобы проверить нашу способность мыслить логически и решать сложные задачи.
Одна из таких задач — как превратить треугольник в квадрат. Это задание, требующее от нас поиска креативных решений и использования различных геометрических принципов.
Существует множество способов преобразования треугольника в квадрат, и некоторые из них могут показаться неочевидными. Варианты могут включать в себя деление и поворот треугольника, соединение точек с разными углами и использование дополнительных геометрических фигур.
Интересно, что это задание постоянно обсуждается и в настоящее время, и различные группы исследователей предлагают свои варианты решения. Таким образом, эта геометрическая загадка стимулирует наше творческое мышление и демонстрирует богатство геометрии во всей ее красе.
Геометрическая загадка: превращение треугольника в квадрат
Переходим к решению загадки. Первый шаг — взять сторону треугольника a и разделить ее на две равные части. Обозначим полученную точку деления как M. Далее, соединяем точку M и точку B, получив отрезок MB. Теперь проводим параллель к отрезку MB через точку A и пересекаем ее с отрезком MC. Обозначим точку пересечения как J. Выделим отрезок AJ, чтобы затем его продлить вдвое и получить точку K на продолжении этого отрезка. Теперь имеем отрезок CK, который является четвертью отрезка AB. Если проделать аналогичные действия с другими сторонами треугольника, то мы получим точки пересечения, образующие квадрат.
Таким образом, геометрическая загадка о превращении треугольника в квадрат может быть решена путем проведения определенной последовательности действий. Ответ заключается в нахождении точек пересечения отрезков, которые позволяют построить квадрат из исходного треугольника. Знание основных принципов геометрии и точный расчет позволяют найти решение этой увлекательной головоломки.
Определение проблемы: от треугольника к квадрату
Возникает увлекательная геометрическая загадка: как можно превратить треугольник в квадрат? Данная задача привлекает внимание математиков и геометров, ставя перед ними необычную задачу преобразования одной фигуры в другую. Однако, несмотря на сложность данной задачи, есть подходы и методы, которые позволяют решить эту загадку.
Первоначально, для решения этой геометрической задачи, следует понять основные свойства треугольника и квадрата. Треугольник — это фигура, состоящая из трех сторон и трех углов, в то время как квадрат имеет четыре равные стороны и прямые углы. Эти различия между треугольником и квадратом являются основными препятствиями преобразования треугольника в квадрат.
Одним из возможных способов решения этой задачи является использование принципа симметрии.
- Возможно использование оси симметрии по отношению к одной из сторон треугольника, чтобы создать соответствующие отображения относительно других сторон.
- Другой подход заключается в разделении треугольника на несколько составных элементов и их последовательном преобразовании для формирования частей квадрата.
- Также можно использовать комплексные преобразования, такие как вращение, сжатие и растяжение, чтобы преобразовать треугольник в квадрат.
Все эти подходы требуют детальных рассуждений, использования математических формул и глубокого понимания геометрии. Решение данной задачи не только развивает логическое мышление и навыки анализа, но и позволяет лучше понять основные принципы геометрии, применяемые в решении подобных задач.
Метод 1: использование диагоналей
Есть удивительный способ превратить треугольник в квадрат, используя только его диагонали. Этот метод позволяет превратить треугольник в прямоугольник, а затем востановить его в квадрат.
Для начала, проведите диагонали в треугольнике, соединяющие вершины. Терпеливый математик заметит, что эти диагонали делят треугольник на четыре прямоугольных треугольника.
Теперь нужно взять эти прямоугольные треугольники и собрать их, чтобы получить квадрат. Это можно сделать, поменяв стороны прямоугольников местами и соединив их вместе. В итоге, вы получите квадрат, который был ранее треугольником.
Метод 2: деление и перестановка сторон
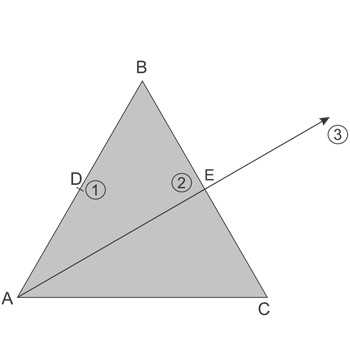
Для того чтобы превратить треугольник в квадрат, можно использовать метод деления и перестановки сторон. Этот метод основан на идее разделения треугольника на две части и перестановки этих частей таким образом, чтобы получить квадрат.
Шаг 1: Возьмите треугольник ABC и проведите линию, проходящую через середину стороны AB и перпендикулярную ей. Таким образом, вы разделите треугольник на две части: треугольник ABE и треугольник ACE, где точка E — середина стороны AB.
Шаг 2: Поверните треугольник ACE на 90 градусов относительно точки E в направлении, противоположном обходу по часовой стрелке. Переместите полученный треугольник вниз на расстояние, равное длине стороны AC.
Шаг 3: Теперь у вас есть две части треугольника, расположенные рядом друг с другом. Соедините точки B и C линией, получившиеся линии AB и BC будут двумя сторонами квадрата. Таким образом, вы превратили треугольник в квадрат.
Этот метод позволяет геометрически преобразовать треугольник в квадрат без использования дополнительных фигур или угловых резцов. Он демонстрирует важность правильного позиционирования и перестановки геометрических фигур для достижения желаемого результата.
Метод 3: использование вписанного квадрата

Шаги данного метода следующие:
- Нарисуйте треугольник на листе бумаги.
- Выберите одну из сторон треугольника и нарисуйте на ее продолжении внешнюю сторону квадрата.
- Постройте прямую, проходящую через середину выбранной стороны треугольника и перпендикулярную к ней.
- Проведите прямые, проходящие через середины двух других сторон треугольника, и перпендикулярные к ним.
- Точки пересечения этих прямых будут вершинами вписанного квадрата.
- На основании вершин вписанного квадрата, проведите стороны квадрата.
- Треугольник преобразован в квадрат.
Таким образом, использование вписанного квадрата позволяет превратить треугольник в квадрат и решить данную геометрическую загадку.
Метод 4: вращение и масштабирование треугольника
Если вы хотите превратить треугольник в квадрат, вы можете воспользоваться методом вращения и масштабирования треугольника. Этот метод позволяет изменить форму и размер треугольника таким образом, чтобы его стороны стали равными и углы прямыми.
Первым шагом в этом методе является вращение треугольника вокруг одной из его вершин на 90 градусов. Затем треугольник масштабируется путем увеличения или уменьшения его размера таким образом, чтобы длина его сторон стала равной. И, наконец, применяется второе вращение, чтобы привести углы треугольника к прямым.
- Вращение треугольника на 90 градусов вокруг вершины A можно осуществить, например, при помощи поворотной матрицы:
| x’ | = | cos(90) | * | (x — A.x) | — | sin(90) | * | (y — A.y) | + | A.x |
| y’ | = | sin(90) | * | (x — A.x) | + | cos(90) | * | (y — A.y) | + | A.y |
- Далее треугольник масштабируется путем изменения длины его сторон. Для этого можно использовать соотношение между длинами сторон исходного треугольника и квадрата.
- Наконец, применяется второе вращение на -90 градусов, чтобы привести треугольник к форме квадрата.
Используя этот метод, вы можете превратить треугольник в квадрат, сохраняя его форму и размеры, но при этом сделав его стороны равными и углы прямыми.
Короткое описание
Метод 4: вращение и масштабирование треугольника — это эффективный способ изменения положения и размеров треугольника на плоскости. Он позволяет вращать фигуру вокруг определенной точки и масштабировать ее без потери пропорций. С помощью метода 4 можно создавать уникальные и креативные дизайны, добавлять динамику и акценты в графические проекты. Также он полезен для анимации и создания интерактивных эффектов. Обладая различными параметрами и настройками, этот метод предлагает множество вариантов для творческой реализации и визуального воздействия. Метод 4: вращение и масштабирование треугольника является одним из основных инструментов в графическом дизайне и веб-разработке, позволяющим создавать уникальные и привлекательные визуальные элементы.
Вопрос-ответ:
Как производится вращение треугольника?
Вращение треугольника производится путем изменения угла его поворота относительно определенной точки, называемой центром вращения.
Что такое масштабирование треугольника?
Масштабирование треугольника представляет собой изменение его размера, путем увеличения или уменьшения длин сторон и углов треугольника.
Какой метод используется для вращения и масштабирования треугольника?
Для вращения и масштабирования треугольника применяется матричная трансформация, при помощи которой можно задать требуемый угол вращения и коэффициент масштабирования.
Что такое матрица трансформации?
Матрица трансформации — это математическая структура, которая позволяет выполнить определенное преобразование, такое как вращение или масштабирование, над геометрическим объектом, в данном случае — треугольником.
Какие параметры можно изменять при вращении и масштабировании треугольника?
При вращении и масштабировании треугольника можно изменять угол поворота, центр вращения, коэффициент масштабирования, а также масштабировать треугольник относительно различных осей координат.


