Математика — это удивительный мир, где числа и формулы создают сложнейшие лабиринты, которые нужно разгадать. Решение математических задачек требует логического мышления, аналитических навыков и терпения. Каждая задача — это новая загадка, которую нужно раскрыть, чтобы попасть к правильному ответу.
Нередко математические задачи содержат в себе запутанные лабиринты чисел, где каждое число и операция имеет свое значение и взаимодействие. Разгадывая эти лабиринты, мы углубляем свое понимание математических закономерностей и приобретаем новые знания. Каждый раз, когда мы находим правильный путь через лабиринт чисел, мы получаем ощущение удовлетворения и достижения.
Решая математические задачки, мы развиваем свою умственную гибкость и способность к абстрактному мышлению. Лабиринты чисел тренируют наше внимание, память и скорость реакции. Каким бы сложным ни был лабиринт, он всегда имеет решение, и наша задача — найти его. В этом процессе мы расширяем свои познания в математике и осваиваем новые методы решения задач.
Когда мы решаем математические задачки, мы не только улучшаем свои навыки в этой области, но и развиваем свою логику и аналитическое мышление. Математика помогает нам лучше понимать мир вокруг нас, а решение задач — это наша возможность разгадать загадки чисел и обрести новые знания. Поэтому не бойтесь лабиринтов чисел, а смело отправляйтесь разгадывать их, открывая новые горизонты математического мира.
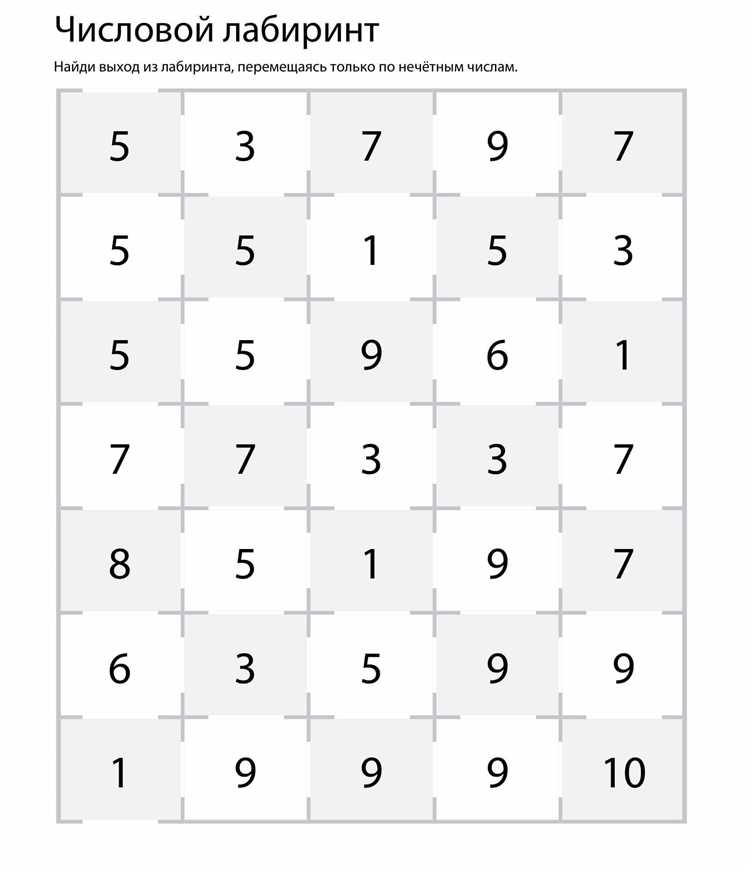
Лабиринты чисел: решаем математические задачки

В лабиринтах чисел каждая цифра имеет свое значение и роль. Путем правильного комбинирования этих цифр и использования математических операций, нужно найти выход из лабиринта. При этом каждый шаг требует тренировки ума, внимательности и навыков работы с числами.
Для решения математических задачек в лабиринтах чисел необходимо собрать всю доступную информацию, а затем применить логику и математические операции, чтобы разгадать загадку. Это отличная тренировка для умственной активности и развития навыков решения сложных задач.
Использование лабиринтов чисел не только увлечет вас в мир математических головоломок, но и поможет вам развить новые подходы к решению задач и добиться успеха в изучении математики. Ведь математика – это не только предмет, но и способ мышления, который пригодится в жизни и поможет вам справиться с разными сложностями.
Сложение и вычитание
Математические операции сложения и вычитания широко используются в повседневной жизни и научных исследованиях. Эти операции позволяют складывать и вычитать числа, что помогает решать различные задачи и находить решения к сложным уравнениям.
Сложение – это операция, которая объединяет два или более числа для получения их суммы. При сложении чисел мы считаем их количество и складываем их значения. Например, если мы складываем числа 4 и 5, то получаем сумму 9. Сложение также можно представить в виде расположения чисел в ряд и нахождения общей длины этого ряда.
Вычитание – это операция, которая позволяет находить разность между двумя числами. При вычитании мы вычитаем одно число из другого и получаем разницу. Например, если мы вычитаем из числа 10 число 3, то получаем разность 7. Вычитание также можно представить в виде удаления элементов из ряда чисел. Как и при сложении, результат вычитания может быть положительным, отрицательным или равным нулю.
Сложение и вычитание являются базовыми математическими операциями, которые необходимо знать и понимать для решения различных задач. Они являются основой для более сложных операций, таких как умножение и деление, и используются как основа для развития математического мышления и логики.
Умножение и деление
Умножение
Умножение — это операция, при которой два числа (множители) преобразуются в третье число (произведение). Оно обозначается знаком умножения «×» или знаком «*», и выполняется путем повторения сложения одного из чисел.
Умножение имеет несколько свойств, таких как коммутативность (порядок множителей не важен), ассоциативность (порядок выполнения умножения не важен) и дистрибутивность (умножение распространяется на сумму или разность).
Деление
Деление — это операция, обратная умножению. Она позволяет разделить одно число (делимое) на другое число (делитель) и получить результат, называемый частным. Оно обозначается знаком деления «÷» или знаком «/».
При делении важно помнить о таких понятиях, как делимое, делитель и частное. Деление также имеет свои правила, например, деление на ноль не определено, и остаток от деления может быть равен нулю или иметь некоторое значение.
Умножение и деление являются основными операциями, которые помогают нам решать математические задачи и проводить различные вычисления. Понимание этих операций позволяет нам разобраться с числами и их взаимосвязью.
Задачи на пропорции
Пропорция состоит из четырех чисел, разделенных на две группы. Каждая группа состоит из двух чисел, где первое число относится ко второму, как третье число относится к четвертому. Проблемы с пропорциями могут включать известные величины, которые необходимо использовать для нахождения неизвестной величины.
Пример задачи
У нас есть пропорция между числами: 5:10 = 8:x. Мы знаем, что первое число равно 5, а второе равно 10. Мы хотим найти значение x. Для того чтобы найти x, мы можем использовать принцип пропорциональности.
Мы можем записать данную пропорцию в виде уравнения: 5/10 = 8/x.
Путем перемножения числителя и знаменателя на x, мы можем сократить уравнение и решить его:
5x = 80.
Делим обе стороны на 5, чтобы найти значение x:
x = 16.
Таким образом, когда 5:10 = 8:x, x равно 16.
Геометрические задачи
Одной из распространенных задач в геометрии является нахождение площади фигуры. Для этого необходимо знать формулы, которые связывают площадь с различными параметрами фигуры, например, площадь прямоугольника равна произведению его сторон, а площадь круга соответствует произведению квадрата радиуса на число Пи.
Еще одной интересной геометрической задачей является нахождение объема тела или его поверхности. Например, для нахождения объема параллелепипеда необходимо перемножить его длину, ширину и высоту. А для нахождения площади поверхности сферы нужно знать радиус и применить соответствующую формулу.
- Треугольники: геометрические фигуры с тремя сторонами. Для решения задач, связанных с треугольниками, полезно знать различные свойства треугольников, такие как равенство углов, соотношения между сторонами и углами, теорему Пифагора и другие.
- Прямоугольники и квадраты: фигуры с прямыми углами и равными сторонами. Задачи, связанные с данными фигурами, могут быть связаны с нахождением площади, периметра или диагонали.
- Окружности: фигуры с равными расстояниями от центра до любой точки на ее окружности. В геометрических задачах может быть необходимо найти длину дуги окружности, площадь круга или радиус, используя различные формулы.
В решении геометрических задач необходимо овладеть навыками работы с различными геометрическими формулами, а также умением логически мыслить и анализировать пространственные объекты. Знание основных свойств и формул позволит успешно решать геометрические задачи и справляться с геометрией в повседневной жизни.
Задачи на проценты
Проценты часто используются в различных ситуациях, например, при расчете скидок, налогов или процентной ставки по кредитам. Понимание основных принципов работы с процентами позволяет более эффективно планировать финансы и прогнозировать результаты операций.
Задачи на проценты могут быть разного уровня сложности. Некоторые из них требуют применения базовых формул, таких как нахождение процента от числа или нахождение числа по проценту от известного числа. Другие задачи могут быть более сложными и требовать применения комбинированных операций с процентами.
Решение задач на проценты можно представить в виде таблицы или схемы, где указывается известная информация и неизвестная величина, которую необходимо найти.
- Важно разобраться в условии задачи и понять, какие данные известны;
- После этого необходимо выбрать подходящую формулу и провести соответствующие вычисления;
- Не забудьте ответить на вопрос задачи и оформить ответ в соответствии с условием.
Решение задач на проценты поможет не только развить математические навыки, но и приобрести практические навыки работы с процентами в реальных ситуациях.
Задачи на логику
Примером задачи на логику может быть следующая ситуация: «Том занимается спортом каждый день, а вчера он не занимался спортом. Верно ли утверждение, что Том занимался спортом сегодня?». Чтобы получить ответ на этот вопрос, мы должны логически рассуждать и применять правила логики, основываясь на информации, данной в условии задачи.
- Применение формальной логики – рассуждения о сущностях и отношениях между ними в рамках данной задачи.
- Логика и рассуждения – анализ информации в задаче, сопоставление фактов и логических заключений на основе этих фактов.
- Анализ условий – разбор условий задачи и выявление заложенных в них подробностей, которые могут повлиять на решение.
Короткое описание
Книга «Задачи на логику» представляет собой набор увлекательных задач, которые помогут развить логическое мышление и способность к аналитическому мышлению. В ней собраны разнообразные головоломки, где придется применять логику, рассуждать, находить закономерности и строить дедукции. Эта книга подходит как для детей, так и для взрослых, кто хочет потренировать свой ум и развить навыки логического мышления.
Вопрос-ответ:
Как решить задачу на логику?
Чтобы решить задачу на логику, нужно анализировать условие, выделять ключевые факторы, применять логические операции и дедуктивное мышление, чтобы прийти к правильному ответу.
Какие бывают типы задач на логику?
Задачи на логику могут быть различных типов, включая логические головоломки, задачи на сравнение и классификацию, задачи на вывод логических утверждений и многое другое.
В чем заключается особенность задач на логику?
Особенность задач на логику заключается в том, что для их решения необходимо применить абстрактное мышление, логическую обработку информации и умение находить связи между фактами и условиями задачи.
Как развить логическое мышление для решения задач?
Для развития логического мышления можно решать задачи на логику, решать головоломки и головоломки, играть в логические игры, изучать логические законы и понятия и тренировать умение анализировать информацию и находить связи между фактами.
Какие преимущества дает развитие логического мышления?
Развитие логического мышления позволяет лучше анализировать информацию, принимать лучшие решения, быстрее решать проблемы, улучшает критическое мышление и способствует развитию креативных навыков.
Как решить задачу на логику типа «Кто в каком доме живёт?»?
Для решения этой задачи нужно использовать информацию, которая уже дается в условии. Обычно условие содержит описание нескольких фактов о людях и их предпочтениях. Нужно внимательно прочитать каждое утверждение и использовать логику, чтобы определить, какие факты могут быть взаимосвязаны и какую информацию можно получить из них. В конечном итоге нужно сравнить все возможные варианты и составить таблицу или схему, чтобы найти решение.
Как решить задачу на логику типа «Кто сколько дал денег?»?
Для решения этой задачи также нужно использовать логику. Обычно в условии описывается сумма, которую дал каждый человек, а также некоторые дополнительные факты и ограничения. Нужно внимательно прочитать каждое утверждение и попытаться вывести из них как можно больше информации. Можно использовать метод проб и ошибок, пытаясь присвоить разные суммы разным людям и проверять, согласуется ли это с остальными фактами. В конечном итоге нужно найти комбинацию сумм, которая соответствует всем условиям задачи.