
Геометрия всегда волновала умы ученых и любителей математики. Одной из интересных геометрических фигур является равнобедренный треугольник. Его особенность заключается в том, что две стороны данной фигуры равны между собой. Если вы готовы разгадывать загадки и применять свои знания геометрии, тогда вперед!
Предлагаем разобраться с несколькими загадками, связанными с равнобедренными треугольниками. Все, что вам потребуется — это внимательность и немного математической логики. Загадки помогут вам лучше понять свойства равнобедренных треугольников и научиться их применять на практике.
Готовы начать? Тогда давайте выясним, насколько вы хорошо знаете геометрию и сможете составить решение этих математических загадок.
Загадки с равнобедренными треугольниками: все ответы в одной статье
Загадка 1:
Два равнобедренных треугольника стоят рядом. Сколько у них общих сторон?
Ответ: Два равнобедренных треугольника имеют только одну общую сторону.
Загадка 2:
Что получится, если пересечь два равнобедренных треугольника друг с другом?
Ответ: При пересечении двух равнобедренных треугольников могут получиться различные фигуры, в зависимости от угла, под которым они пересекаются. Например, это может быть параллелограмм или ромб.
Загадка 3:

Какое количество углов у равнобедренного треугольника?
Ответ: Равнобедренный треугольник имеет три угла, как и любой другой треугольник.
Загадка 4:
Что можно сказать о длинах сторон в равнобедренном треугольнике?
Ответ: В равнобедренном треугольнике две стороны равны по длине, а третья сторона может быть различной.
Загадка 5:
Как найти площадь равнобедренного треугольника?
Ответ: Площадь равнобедренного треугольника можно найти, зная длину основания и высоту, опущенную на это основание. Формула для расчета площади равнобедренного треугольника: S = (b * h) / 2, где b — длина основания, h — высота.
Загадка №1: Найди длину основания равнобедренного треугольника
Решая данную геометрическую загадку, мы сталкиваемся с задачей определения длины основания равнобедренного треугольника. Чтобы найти эту длину, нам необходимо обратиться к свойствам и особенностям такого треугольника.
Равнобедренный треугольник имеет две равные стороны и два равных угла. Для нахождения длины основания у нас есть несколько методов, которые мы можем использовать. Один из них — использование теоремы Пифагора или применение свойств треугольников с прямыми углами.
- Применение теоремы Пифагора: если известны длины равных сторон треугольника и мы знаем длину его высоты (проведенной из вершины до основания), то можем применить теорему Пифагора для нахождения основания.
- Использование свойств треугольников с прямыми углами: если у нас есть другие данные о треугольнике, например, известен один из углов треугольника, то мы можем использовать тригонометрические функции для расчета длины основания.
В обоих случаях для решения загадки необходимо знание геометрических основ и использование соответствующих формул. Результатом будет определение длины основания равнобедренного треугольника, который является одним из основных параметров этой фигуры.
Условие загадки
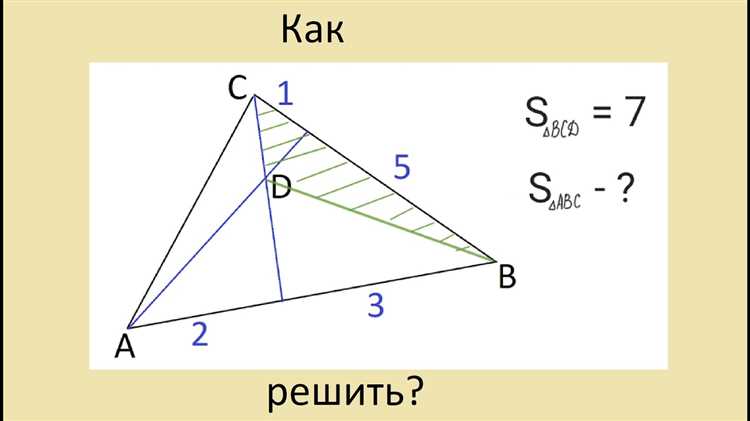
У нас есть загадка, связанная с равнобедренными треугольниками. Чтобы решить эту загадку, нам необходимо проанализировать заданную информацию и найти правильный ответ. Погрузимся в геометрические вычисления!
Загадка состоит в следующем: у нас есть равнобедренный треугольник, в котором известны значения двух сторон и угол между ними. Наша задача — найти значение третьей стороны и двух оставшихся углов треугольника.
Для решения этой загадки мы можем использовать различные формулы и свойства равнобедренных треугольников. Например, мы знаем, что у равнобедренного треугольника две стороны равны между собой. Также у нас есть угол между этими сторонами, что позволяет нам использовать закон синусов или косинусов для нахождения значения третьей стороны и углов треугольника.
Таким образом, чтобы решить эту загадку, нам необходимо правильно применить геометрические формулы и использовать свойства равнобедренного треугольника. Готовы ли вы взяться за решение этой загадки и найти правильный ответ?
Подсказка:
В задачах с равнобедренными треугольниками важно обратить внимание на особенности этого вида треугольников. Все равнобедренные треугольники имеют две равные стороны. Это означает, что углы, противоположные этим сторонам, также будут равными. При решении задач по геометрии с равнобедренными треугольниками можно использовать это свойство для нахождения значений углов и сторон.
Если в задаче дан один угол равнобедренного треугольника и одна его сторона, можно легко найти все остальные стороны и углы. Для этого можно использовать соответствующие геометрические формулы, такие как теорема синусов и теорема косинусов. Важно не забыть, что у равнобедренного треугольника две стороны равны, поэтому можно использовать это свойство для поиска неизвестных значений.
Ответ
Решая загадки с равнобедренными треугольниками, мы должны знать, что такой треугольник имеет две равные стороны и два равных угла. Какой ответ мы ищем в каждой конкретной загадке, зависит от предоставленных данных и требований.
Разбираемся в конкретной загадке, чтобы найти ответ. Ищем информацию о равнобедренном треугольнике и выясняем, какие углы и стороны даны. Далее применяем геометрические законы и формулы к предоставленным данным, чтобы получить искомый результат. Ответом может быть длина стороны, величина угла или какая-то другая характеристика треугольника.
Иногда ответ может быть не единственным, и мы должны уточнить, какую информацию ищем. Например, если нам даны длины двух сторон равнобедренного треугольника, мы можем найти длину третьей стороны с использованием теоремы Пифагора. Однако, чтобы найти углы треугольника, нам понадобится дополнительная информация, например, высота или угол между сторонами. В таком случае мы должны уточнить, ищем ли мы длины сторон или величину углов.
Загадка №2: Определение высоты равнобедренного треугольника
Чтобы определить высоту равнобедренного треугольника, можно воспользоваться теоремой Пифагора или использовать формулу для вычисления площади треугольника. Если известны длина основания и высота, то можно найти площадь треугольника и затем высоту.
Также высота равнобедренного треугольника может быть найдена с помощью тригонометрических функций. Например, если известны угол и длина основания, можно использовать тангенс угла, чтобы найти высоту треугольника.
Определение высоты равнобедренного треугольника является важным для решения различных задач, связанных с этой геометрической фигурой. Знание высоты позволяет находить площадь треугольника, находить его центр тяжести и определять различные свойства треугольника.
Условие загадки
В равнобедренном треугольнике имеется два основания и две равные стороны. Найдите ответ на загадку, решив геометрическую задачу.
В данном случае у вас есть равнобедренный треугольник, в котором угол при вершине равен 70 градусам. Ваша задача — найти значение угла при основании треугольника. Какое значение этого угла?
Подсказка
Для решения загадок с равнобедренными треугольниками полезно знать основные свойства этого вида треугольников.
Например, если в условии указано, что две стороны равны, а третья сторона неизвестна, значит, третья сторона тоже равна уже известной. Или если указано, что два угла треугольника равны, то их противолежащие стороны также равны.
Важно заметить, что если ты знаешь только одно из условий о треугольнике, это еще не достаточно для полного решения задачи. Но это может стать полезной подсказкой и направить тебя на правильный путь к ответу.
Вопрос-ответ:
Как использовать подсказку при написании текста?
Для использования подсказки при написании текста необходимо достаточно подробно описать проблему или задачу, с которой возникли трудности. Затем указать ключевые слова или фразы, по которым нужно получить подсказку.
Какие типы подсказок бывают?
Подсказки могут быть различных типов: текстовые, графические, видео и аудио. Текстовые подсказки представляют собой небольшие пояснения и советы, графические — изображения или схемы, видео — видеоролики с пошаговыми инструкциями, а аудио — аудиозаписи с разъяснениями.
Сколько подсказок можно получить по одной проблеме?
Количество подсказок, которые можно получить по одной проблеме, может быть разным. Возможно, первая подсказка будет достаточно, чтобы решить проблему, но иногда приходится получать несколько подсказок, пока не будет найдено решение.
Какая информация должна быть в подсказке?
Подсказка должна содержать информацию, которая поможет пользователю решить проблему или выполнить задачу. В ней может быть описание шагов, которые нужно выполнить, указание на ошибки, которые могут возникнуть, или дополнительные советы для более эффективного решения.
Где можно получить подсказки?
Подсказки можно получить в различных источниках: на сайтах, в книгах, в видеоуроках, в форумах и блогах, а также у других пользователей и специалистов в данной области. Также существуют специальные приложения и программы, которые предлагают подсказки по конкретным задачам.
Что такое подсказка?
Подсказка — это информация или подсказка, предоставляемая для помощи в выполнении определенного действия или решении определенной задачи.


