
Любители головоломок и занимательных задач могут насладиться умственным творчеством, решая самые сложные головоломки, основанные на логике. Такие задачи требуют не только сообразительности, но и логического мышления.
Среди самых известных головоломок основанных на логике можно выделить задачу о взвешивании. В этой задаче требуется найти один фальшивый монету из группы монет, которые различаются по весу. Задача состоит в том, чтобы с помощью ограниченного числа взвешиваний на чашечных весах найти эту фальшивую монету. Для решения этой задачи необходимо использовать логику и методы последовательного исключения.
Еще одной интересной головоломкой, основанной на логике, является задача о светофорах. В этой задаче требуется найти оптимальную последовательность перемещений для проезда через несколько светофоров, которые работают независимо друг от друга. Задача состоит в том, чтобы пройти маршрут с минимальной задержкой. Для решения этой задачи необходимо использовать логическое мышление и анализ.
Логические головоломки представляют собой увлекательное и полезное занятие, которое развивает умственные способности и помогает тренировать логическое мышление. Решая такие задачи, можно научиться логически мыслить, принимать взвешенные решения и находить нестандартные пути решения проблем. Помимо развития интеллектуальных навыков, решение логических головоломок может принести удовлетворение и радость от решения сложных задач.
Представьте себе увлекательный мир головоломок, основанных на логике. Известные игры такие, как Шашки, Шахматы, Судоку и Механический кубик, требуют от игрока способности мыслить логически и стратегически. Они становятся популярными вызовами для ума, привлекая множество игроков по всему миру.
Другой популярной головоломкой, основанной на логике, является «Змейка». Ее целью является заполнение каждой клетки игрового поля змейкой, не пересекая линии и закрывая области, ограниченные заранее заданными правилами. Игроку нужно логически рассуждать и находить правильные шаги, чтобы решить головоломку и достичь требуемого результата.
В игре «Правда или Ложь» игрокам предлагается ряд утверждений, и их задачей является определить, является ли каждое утверждение истинным или ложным. Эта головоломка требует логического мышления, анализа и оценки различных факторов для правильной классификации утверждений. Игра является популярной из-за своей простоты и способности развивать умение логического мышления и аналитического принятия решений.
Головоломка Эйнштейна
Например, головоломка может звучать так:
- В пяти домах каждый житель пьет разный напиток, курит разные сигареты, держит разных животных, и все они разных национальностей. Вопрос: Кто пьет воду?
- У одного из соседей есть рыбка.
Решение головоломки – сложная задача, требующая внимания к деталям, аналитического мышления и умения логически рассуждать. Загадка Эйнштейна стала настоящим испытанием для многих людей и позволяет не только потренировать умственные способности, но и развить логику и креативное мышление.
Задача с пятью свадьбами
В условии головоломки указано, что пять разных супругов, Федор, Олег, Никита, Алексей и Павел, поженились в разные дни недели, от понедельника до пятницы. Каждый супруг имеет свою профессию: программист, банкир, юрист, учитель и врач. К условиям также добавлены различные уточнения, связанные с порядком их свадеб.
С помощью анализа различных условий и элиминации возможных вариантов, можно прийти к правильному решению головоломки. Необходимо учитывать фразы, как то: тот, кто заключил брак с Лизой, поженился в понедельник; банкир женился во вторник; жена врача стала госсекретарем после свадьбы и так далее. Путем исключения и сравнения условий, можно установить верные сочетания имени, профессии и дня свадьбы.
Задача про три шляпы
Представьте себе, что перед вами стоят три шляпы – одна красная, одна синяя и одна зеленая. Под каждой шляпой находится карточка, но вы не знаете, какая именно. На каждой карточке написано цвет соответствующей шляпы. Задача состоит в том, чтобы угадать, какой цвет находится под каждой шляпой.
Изначально предположим, что у вас нет никакой информации о цветах шляп. Однако, есть несколько правил, которые можно использовать для угадывания. Правило номер один: каждая шляпа имеет свой цвет и никаких шляп с одинаковым цветом не существует. То есть, красная шляпа не содержит карточку с надписью «красный», и так далее.
Проверка гипотезы
Вам предоставляется возможность сделать одно единственное предположение о цветах шляп. Нужно продумать гипотезу и рационально выбрать шляпу, под которой, как вы полагаете, находится та карточка, на которой написан цвет правильной шляпы.
- Рассмотрим различные сценарии и соответствующие предположения:
- Смелая гипотеза: Вы предположили, что карточка под красной шляпой имеет надпись «зеленый».
- Осторожная гипотеза: Вы предположили, что карточка под зеленой шляпой имеет надпись «синий».
- Аудациозная гипотеза: Вы предположили, что карточка под синей шляпой имеет надпись «красный».
Принимая предположение, вы указываете на конкретную шляпу, которую считаете правильной. Затем вам сообщают, правильно ли вы угадали цвет шляпы или нет.
Взяв в расчет все возможные варианты, вы сможете разгадать эту головоломку и достичь своей цели. Задача про трех шляпы считается одной из самых интересных и интеллектуально развивающих головоломок, которая требует глубокого анализа и логического мышления.
Головоломка «Шарики и шашки»
Одна из самых известных головоломок, основанных на логике, называется «Шарики и шашки». Головоломка представляет собой игровое поле с разными цветными шариками и шашками. В центре поля находится колонка, в которую можно помещать шарики определенных цветов.
Цель головоломки состоит в том, чтобы поставить все шарики в колонке в определенном порядке, используя доступные шашки. Правила головоломки могут варьироваться в зависимости от конкретной версии игры, но обычно игроку разрешается передвигать шарики только с определенными ограничениями и в определенном порядке.
Популярность этой головоломки объясняется ее простотой и одновременно сложностью. Перемещение шариков и шашек требует стратегического мышления и планирования, а также умения видеть долгосрочные последствия своих действий. Головоломка «Шарики и шашки» может быть очень увлекательной и вызывать интерес у разных возрастных групп.
Решение этой головоломки требует глубокого анализа и поиска оптимальных ходов. Игрок должен обдумывать каждое свое действие, чтобы убедиться, что его решение приведет к желаемому результату. Возможно существуют разные стратегии, ведущие к решению головоломки, и игрок должен пробовать разные варианты, чтобы найти оптимальный подход к решению задачи.
Пример задачи:
- Имеется игровое поле с 5 разноцветными шариками и 3 шашками.
- Цель состоит в том, чтобы поместить шарики в колонку в следующем порядке: синий, зеленый, красный, желтый, фиолетовый.
- Правила разрешают передвигать шарики только с помощью шашек, и это можно делать только в определенной последовательности.
- Перемещение шариков и шашек требует стратегического мышления и планирования.
Решение этой задачи может потребовать нескольких ходов и тщательного анализа каждого действия. Интерес головоломки «Шарики и шашки» заключается в том, что она требует от игрока способности прогнозировать будущие последствия своих решений и принимать решения на основе этой информации.
Задача «Умные идентификаторы»
Задача состоит в следующем: необходимо создать систему идентификации, которая будет предоставлять уникальные идентификаторы для объектов разного класса. При этом каждый идентификатор должен быть понятным и информативным, так чтобы можно было быстро идентифицировать объект по его идентификатору.
Для решения этой задачи требуется учитывать разные аспекты, такие как специфика объектов, требования пользователей, а также эффективность и удобство использования системы. Важно создать такую систему, которая будет легко воспринимаема и эффективна в использовании.
Варианты решения головоломки могут быть разнообразными и включать в себя различные подходы и алгоритмы. Однако, важно учитывать связь между идентификатором и объектом, чтобы они были логически связаны и информативны. Такая система идентификации может найти применение в различных сферах, от учета товаров на складе до идентификации пациентов в медицинской системе.
Головоломка «Умные идентификаторы» требует не только логического мышления, но и креативности в поиске оптимального решения. Она является отличным тренировочным упражнением для развития логического мышления и способности к абстрактному мышлению. В процессе решения этой задачи можно развить свою интуицию, логическое мышление и способность к анализу и синтезу информации.
Задача с вагонами
Всем известна классическая головоломка про вагоны, которая проверяет логическое мышление и способность решать сложные задачи. Данная головоломка состоит в том, чтобы правильно расставить порядок вагонов на железнодорожном пути. Каждый вагон имеет свой уникальный номер, и необходимо упорядочить их так, чтобы получилась правильная последовательность от 1 до N.
Для успешного решения этой задачи необходимо учитывать правила, на основании которых формируется правильная последовательность вагонов. Во-первых, вагоны могут двигаться только вперед, то есть нельзя перемещать вагоны назад. Во-вторых, можно перемещать только вагоны, находящиеся в конце пути. В-третьих, вагоны перемещаются только в одну сторону.
Сложность головоломки заключается в том, чтобы определить правильную последовательность действий, чтобы достичь нужного результата. Это требует логического анализа и попыток перестановки вагонов, чтобы найти наиболее эффективный способ решения.
Пример решения задачи:
Допустим, у нас есть достопримечательность с 5 вагонами, пронумерованными от 1 до 5. Изначально они расположены в произвольном порядке: 3, 1, 5, 2, 4. Чтобы упорядочить их, нужно сделать следующие шаги:
- Переместить вагон 3 на конец пути, чтобы получилась последовательность: 1, 5, 2, 4, 3.
- Переместить вагон 1 на конец пути, чтобы получилась последовательность: 5, 2, 4, 3, 1.
- Переместить вагон 5 на конец пути, чтобы получилась последовательность: 2, 4, 3, 1, 5.
- Переместить вагон 2 на конец пути, чтобы получилась последовательность: 4, 3, 1, 5, 2.
- Переместить вагон 4 на конец пути, чтобы получилась правильная последовательность: 3, 1, 5, 2, 4.
Таким образом, правильный порядок вагонов будет следующим: 1, 2, 3, 4, 5. Используя логическое мышление и последовательность действий, можно успешно решить задачу с вагонами.
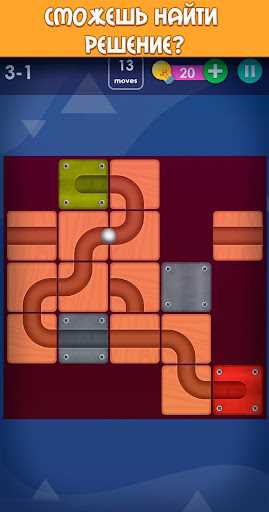
Короткое описание
«Задача с вагонами» — увлекательная головоломка, в которой необходимо правильно расставить вагоны на железнодорожном пути. Тебе предстоит использовать свою логику и пространственное мышление, чтобы определить, какие вагоны должны быть передвинуты, чтобы путь был свободным. В этой игре ты можешь потренировать не только свою память, но и улучшить свои навыки решения проблем, а также научиться принимать решения в условиях ограниченного пространства. Решая задачу, ты сможешь развить логическое мышление, улучшить свою концентрацию и научиться видеть скрытые связи и взаимосвязи между объектами.
Вопрос-ответ:
Чему равно количество вагонов по формуле?
Количество вагонов равно произведению количества перегородок на 6 и прибавлению 1. Формула выглядит так: количество_вагонов = количество_перегородок * 6 + 1.
Сколько вагонов будет, если есть 10 перегородок?
Если есть 10 перегородок, то по формуле получим: количество_вагонов = 10 * 6 + 1 = 61. Таким образом, будет 61 вагон.
Можно ли узнать количество перегородок по заданному количеству вагонов?
Количество перегородок можно найти, подставив заданное количество вагонов в формулу и решив уравнение. Уравнение будет иметь вид: количество_вагонов = количество_перегородок * 6 + 1. Например, если задано количество вагонов 37, то можно решить уравнение: 37 = количество_перегородок * 6 + 1. Решением этого уравнения будет количество перегородок, равное 6.
Как найти количество вагонов, если известна только общая длина поезда и длина одного вагона?
Если известна общая длина поезда и длина одного вагона, то необходимо разделить общую длину на длину вагона и вычесть 1. Формула будет выглядеть так: количество_вагонов = общая_длина_поезда / длина_вагона — 1.
Для чего используются перегородки в вагонах?
Перегородки в вагонах используются для разделения внутреннего пространства на отдельные отсеки или купе, каждое из которых предназначено для размещения пассажиров. Перегородки обеспечивают удобство и комфорт во время поездки, а также позволяют разделить пассажиров на группы и обеспечить им отдельные места для сидения или сна.


