Математика всегда приходила к новым открытиям и вызывала интерес в нас. Одной из самых увлекательных областей математики является геометрия. И среди её головоломок и тайн приходит понимание о многогранниках — объектах, которые обладают странными и захватывающими свойствами. Многогранники — это фигуры, состоящие из множества многоугольных граней, образующих замкнутую поверхность.
Многогранники притягивают внимание математиков уже не одно столетие, их свойства и характеристики изучаются и исследуются с применением различных методов и техник. Геометрия многогранников — это задача нахождения способов описания и классификации данных фигур, а также изучение их внутренних и внешних характеристик.
Одной из самых известных и загадочных головоломок в геометрии является задача о построении планарных многогранников. Это означает, что все грани многогранника должны быть плоскими, а их ребра не должны пересекаться. Такой многогранник является одним из самых сложных и интересных объектов в математике, и его изучение представляет собой не только теоретическую задачу, но и настоящую головоломку для математиков.
Таинственные многогранники: головоломка для математиков
Многогранники делятся на несколько классов в зависимости от своей структуры: правильные, полуправильные и произвольные. Правильные многогранники, такие как тетраэдр, куб или икосаэдр, имеют равные грани и углы, что делает их особенно интересными изучать. Полуправильные многогранники, такие как додекаэдр или октаэдр, имеют различные грани и углы, но сохраняют определенную симметрию. Произвольные многогранники не имеют никаких ограничений и представляют собой наиболее сложные для анализа.
Основная цель математиков состоит в том, чтобы понять структуру многогранников, выявить их свойства и установить взаимосвязи между ними. Изучение этих фигур требует глубокого анализа и применения различных методов, таких как теория графов, топология и геометрическая алгебра. Результаты исследований многогранников имеют важное практическое значение и находят применение в различных областях, включая химию, физику и компьютерную графику.
Таким образом, таинственные многогранники представляют собой настоящую головоломку для математиков. Их структура и свойства вызывают интерес и открывают новые возможности для исследования геометрии. Изучение этих фигур требует применения математического аппарата и творческого подхода. Все это делает мир многогранников увлекательным и волнующим для математиков, которые стремятся раскрыть их геометрические и алгебраические тайны.
Определение многогранников
Многогранники бывают различных форм и размеров. Они могут быть простыми или сложными, симметричными или асимметричными. Для классификации многогранников используют такие характеристики, как количество граней, ребер и вершин.
Гранями многогранников называются его плоские поверхности, ограниченные ребрами. В случае правильных многогранников все грани являются одинаковыми многоугольниками, одинаковыми по количеству сторон и углов. Ребра соединяют вершины и образуют границы граней, а вершины являются точками сходства ребер.
Многогранники играют важную роль в математике и геометрии. Они широко используются в различных областях, таких как физика, химия, информатика и архитектура. Изучение многогранников помогает понять глубинные законы строения и взаимодействия объектов в трехмерном пространстве.
Свойства и классификация многогранников

Свойства многогранников могут включать количество вершин, ребер и граней, их форму, размеры и взаимное положение. Многогранники также могут быть классифицированы на основе различных характеристик, таких как численность и вид их граней.
-
По численности граней: многогранники могут быть классифицированы как правильные, если все грани равновелики и равноугольны, или неправильные, если имеют разные типы граней.
-
По виду граней: многогранники могут быть классифицированы как правильные выпуклые, если все грани являются выпуклыми многоугольниками, или неправильные, если имеют хотя бы одну невыпуклую грань.
-
По форме: многогранники могут быть классифицированы на основе своей формы, такие как призмы, пирамиды или полиэдры.
Классификация многогранников позволяет исследовать их особенности и установить связи между различными типами многогранников. Это имеет важное значение в различных областях, таких как математика, физика, компьютерная графика и топология.
Знаменитые примеры многогранников

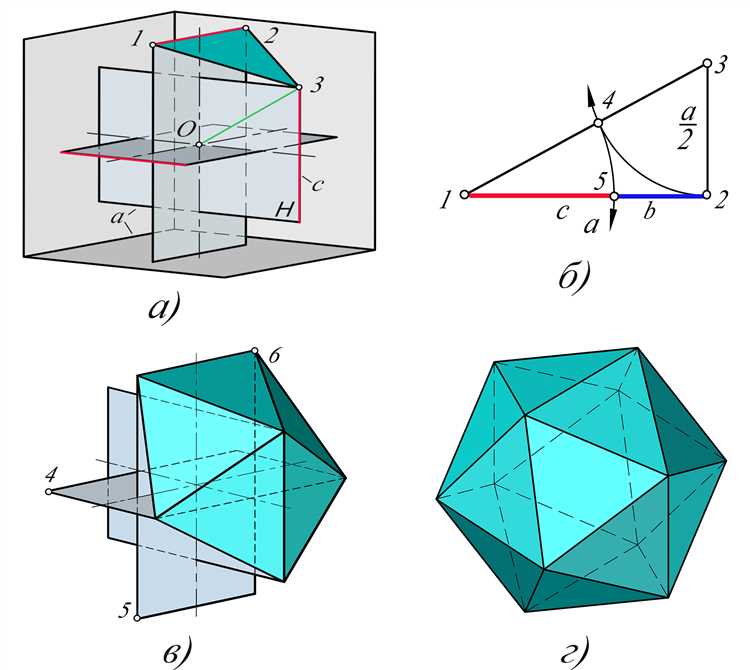
Один из знаменитых примеров многогранников — это икосаэдр. Икосаэдр имеет 20 граней, состоящих из равносторонних треугольников, и 12 вершин. Этот многогранник имеет симметрию высокого порядка и является одним из пяти «платоновских» многогранников, которые были изучены древнегреческими философами.
Еще одним знаменитым примером является куб, который является одним из простейших многогранников. Куб имеет 6 граней, состоящих из квадратов, и 8 вершин. Этот многогранник обладает симметрией по отношению к трехмерным вращениям и используется в архитектуре, играх и графике для создания трехмерных моделей.
Научное изучение многогранников продолжается до сих пор, и каждый новый пример позволяет лучше понять характеристики и свойства этих удивительных геометрических объектов. Знакомство с знаменитыми примерами многогранников помогает расширить наше понимание геометрии и применить это знание в практических задачах.
Возможность существования определенных геометрических форм в виде многогранников долгое время волновала умы математиков. Предположение, выдвинутое Леонардом Эйлером в 1750 году, стало первым шагом к решению этой загадки. Гипотеза Эйлера заключается в том, что для любого выпуклого многогранника, образованного гранями, вершинами и ребрами, выполняется равенство: число вершин плюс число граней минус число ребер равно двум. Другими словами, если мы знаем количество вершин, граней и ребер многогранника, то можно вычислить остальные значения по формуле Эйлера.
Гипотеза Эйлера о многогранниках имела большое значение для развития геометрии и математики в целом. Она способствовала исследованию и классификации различных многогранников, а также позволила находить новые многогранники, удовлетворяющие формуле Эйлера. Эта гипотеза является основой многих теоретических и практических исследований в области геометрии и топологии. Она также нашла применение в других науках, таких как химия и материаловедение, где многогранники используются для изучения структуры и свойств веществ.
Гипотеза Эйлера о многогранниках продолжает быть активно исследуемой и обсуждаемой в настоящее время. Математики стремятся найти доказательство этой гипотезы для всех возможных многогранников и установить ее точные границы. Различные области математики вносят свой вклад в исследование гипотезы Эйлера, создавая новые методы и техники для анализа многогранников. Подтверждение или опровержение этой гипотезы может привести к открытию новых закономерностей и принципов в геометрии и топологии, а также иметь практическое применение в различных областях науки и технологии.
Применение многогранников в науке и технологиях
Одной из областей, где многогранники находят применение, является компьютерная графика. Многогранники используются для создания трехмерных моделей объектов. Они помогают разработчикам визуализировать и анализировать сложные формы и структуры, такие как архитектурные постройки, молекулы и промышленные детали. Это также полезно в игровой индустрии, где многогранники используются для создания реалистичных трехмерных моделей персонажей и окружающей среды.
Кристаллография — еще одна область науки, где применение многогранников крайне важно. Многогранники помогают исследователям анализировать и классифицировать кристаллические структуры различных материалов. Они помогают в определении симметрии кристалла, выявлении особых структурных свойств и предсказании его поведения в различных условиях. Это имеет применение в различных областях, таких как материаловедение, геология и биология.
Таким образом, многогранники играют важную роль в науке и технологиях, способствуя более глубокому исследованию и пониманию сложных форм и структур. Их использование в компьютерной графике и кристаллографии помогает ученым и инженерам решать различные задачи и создавать новые технологии для прогресса и развития в различных областях.
Интересные факты о многогранниках
Вот несколько интересных фактов о многогранниках:
- Граней может быть разное количество: Многогранники могут иметь различное количество граней, начиная от трех и бесконечно увеличиваясь. Некоторые многогранники имеют десятки, сотни и даже тысячи граней, что делает их структуру очень сложной.
- Уникальные имена: Каждый многогранник имеет уникальное имя в зависимости от формы и количества его граней. Некоторые известные примеры включают тетраэдр, куб, октаэдр и додекаэдр.
- Сила в симметрии: Многогранники обладают высокой степенью симметрии. Многие из них могут быть перевернуты, повернуты или отражены без изменения своей формы. Это делает их особенно интересными для изучения и анализа.
- Использование в науке: Многогранники имеют практическое применение в различных областях науки и технологии. Например, они используются в структурной геологии для моделирования кристаллических структур и в компьютерной графике для создания трехмерных объектов.
- Загадочные круги Эйлера: Круги Эйлера – это загадки, связанные с многогранниками. Вопрос о том, сколько существует многогранников с определенным количеством граней, ребер и вершин, является известной головоломкой, изучаемой в математике.
Короткое описание
Интересные факты о многогранниках — это увлекательный набор фактов и информации о геометрических фигурах, которые имеют более трех граней. В этой книге вы узнаете, что многогранники бывают разных форм и размеров, некоторые из них имеют странные или удивительные свойства. Узнайте, какие многогранники являются самыми известными, самыми сложными или самыми простыми. Откройте для себя мир геометрии и узнайте, какие интересные факты скрываются в этих многогранниках.
Вопрос-ответ:
Какие бывают многогранники?
Существуют различные виды многогранников, включая пирамиды, призмы, параллелепипеды, тетраэдры, октаэдры, додекаэдры и многие другие.
Как вычислить объем многогранника?
Для вычисления объема многогранника необходимо знать его форму и размеры. В зависимости от формы, объем может быть вычислен с помощью соответствующих формул, таких как для параллелепипеда — длина х ширина х высота, для пирамиды — площадь основания х высота, и т.д.
Как можно классифицировать многогранники?
Многогранники могут быть классифицированы по различным критериям, таким как количество граней, количество вершин, количество ребер и т.д. Например, треугольники классифицируются как многогранники с тремя гранями, тремя вершинами и трех ребрами.
Можно ли построить многогранник с произвольным числом граней?
Теоретически, многогранники могут иметь любое количество граней, но на практике конкретные виды многогранников ограничены определенным числом граней. Например, существует бесконечное количество треугольных пирамид, но только пять правильных платоновских тел.