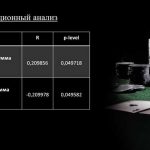
Геометрические проекции — захватывающая тема, которая заставляет нас задуматься о пространственных отношениях. Они представляют собой способ представления трехмерных объектов на плоскости, создавая при этом иллюзию глубины и объема. Но как их интерпретировать?
В данной статье мы попытаемся разгадать загадку геометрических проекций. Рассмотрим различные типы проекций, такие как ортографическая, аксонометрическая и перспективная, и выясним их особенности и применение.
Ортографическая проекция позволяет нам видеть объекты с разных сторон, давая полное представление о их форме и размере. Аксонометрическая проекция, в свою очередь, создает иллюзию трехмерности, сохраняя пропорции объекта. А перспективная проекция придает объектам глубину и реалистичность, соответствующую их расположению в пространстве.
Таким образом, разгадка загадки геометрических проекций заключается в том, чтобы уметь интерпретировать эти различные проекции и использовать их для достижения нужного эффекта. Вперед, давайте вместе исследуем мир геометрических проекций и расшифруем их секреты!
Обзор различных проекций
Проекции играют важную роль в геометрии, архитектуре и дизайне. Они позволяют представить трехмерные объекты на плоскости с различных точек зрения, что помогает в их анализе и конструировании. Существует несколько разных видов проекций, каждая из которых имеет свои особенности и применение.
Одной из наиболее распространенных проекций является параллельная проекция. В этом виде проекции параллельные линии на трехмерном объекте проецируются на плоскость параллельно самим линиям. Это создает плоское изображение, где все параллельные линии сохраняют свои параллельные отношения. Параллельная проекция часто используется в архитектурном проектировании, где точное представление размеров и форм объекта является важным.
Другим видом проекции является перспективная проекция, которая имитирует тот вид, который мы видим в реальной жизни. В этом виде проекции параллельные линии на трехмерном объекте сходятся в одной точке на плоскости проекции, создавая иллюзию глубины и перспективы. Перспективная проекция часто используется в искусстве и графическом дизайне для создания реалистичных изображений.
Таблица сравнения различных проекций

| Вид проекции | Описание | Применение |
|---|---|---|
| Параллельная проекция | Проецирует параллельные линии на плоскость параллельно самим линиям | Архитектурное проектирование |
| Перспективная проекция | Создает иллюзию глубины и перспективы путем схождения параллельных линий в одной точке | Искусство и графический дизайн |
Это лишь некоторые из основных видов проекций, используемых в геометрии и других областях. Каждая проекция имеет свои преимущества и недостатки в зависимости от контекста и требований проекта. Понимание различных проекций является важным навыком для всех, кто занимается визуальным представлением объектов в двух или трех измерениях.
Проекция в плоскость
Существуют разные типы проекций, включая ортогональные и перспективные. В ортогональной проекции параллельные линии в трехмерном объекте отображаются параллельно на плоскости. Этот тип проекции часто используется в технических чертежах и архитектурных планах. В перспективной проекции линии сходятся в одной точке, создавая эффект глубины и объема. Она наиболее реалистично отображает объекты как мы видим их в реальном мире.
- Ортогональная проекция позволяет более точную оценку размеров и форм объекта.
- Перспективная проекция придает изображению глубину и объем.
- Проекции используются в различных областях, включая инженерное дело, архитектуру, компьютерную графику и искусство.
- Правильное использование проекции позволяет более полно и точно передавать информацию о трехмерных объектах.
В зависимости от цели и задачи, выбор типа проекции может быть разным. Ортогональная проекция предпочтительна для измерений и планирования, а перспективная проекция может быть использована для создания впечатляющих и реалистичных визуализаций в искусстве и дизайне.
Проекция на поверхность
При проецировании объекта на поверхность происходит сжатие исходной трехмерной формы в одну плоскость, что позволяет нам увидеть его в двумерном представлении. Такие проекции могут быть выполнены различными способами, включая перспективу и ортогональные проекции.
Одной из основных целей проекции на поверхность является точное и понятное изображение объекта. Она помогает представить его размеры, форму и расположение в двумерном пространстве. Благодаря проекциям на поверхность можно проанализировать объект, изучить его детали и взаимное расположение элементов, а также визуализировать его в различных ракурсах.
Проекция в трехмерном пространстве
Основными видами проекций в трехмерном пространстве являются ортогональная проекция и перспективная проекция. В ортогональной проекции все линии, параллельные какой-либо плоскости проекции, проецируются в параллельные линии на плоскости изображения. Это позволяет точно измерять расстояния и углы в проекции. Перспективная проекция, наоборот, имитирует изображение с использованием угла обзора и позволяет создавать впечатление глубины и объемности объектов.
Ортогональная проекция
Одной из основных техник ортогональной проекции является проекция параллельных проекционных линий. По оси источника света параллельных проекционных линий, представляющих заданные точки, находящиеся на некотором расстоянии от этой оси, можно давать проекции на некоторой плоскости. Трехмерные объекты на этой плоскости суть и есть их проекции. Проекции заданных точек находят посредством параллельного пересечения проекционных линий и плоскости.
Интерпретация фигур в различных проекциях
Фигуры, представленные в различных проекциях, могут иметь разные визуальные характеристики и вызывать различные ассоциации у наблюдателя. Интерпретация фигур может зависеть от выбранного угла обзора и способа представления.
Например, если рассматривать геометрическую фигуру в плоской проекции, она может выглядеть как простой многоугольник, состоящий из различных сторон и углов. Однако, при изменении проекции и наклона фигуры, она может приобретать новое значение и интерпретацию. Фигура может быть воспринята как объемный объект, имеющий объем и глубину.
Интерпретация фигур также может зависеть от контекста и цели использования. Например, геометрическая фигура в проекции может использоваться для представления здания или объекта в архитектуре. Она может служить для визуализации пространственных отношений и деталей конструкции.
При анализе и интерпретации фигур в различных проекциях важно учитывать их форму, пропорции, углы и взаимное расположение элементов. Также следует учитывать параметры проекции, такие как освещение, тени и перспективу, которые могут влиять на восприятие фигуры и создавать иллюзию объема и глубины.
Интерпретация фигур в различных проекциях требует внимания к деталям и умения видеть объекты с разных сторон и в разных ракурсах. Это позволяет получить более полное представление о форме и структуре фигуры, а также понять ее функциональность и значение в соответствующей области знания или творчества.
Как анализировать фигуры в 2D проекции?
Формы и фигуры в плоской проекции могут быть интерпретированы с помощью нескольких аспектов: размеров, пропорций и расположения. Наблюдение и анализ этих характеристик позволяет более точно понять значение и назначение представленной фигуры.
Во-первых, размеры фигуры играют важную роль. Они могут указывать на разные атрибуты, такие как величина объекта, его структура или функциональность. Крупные размеры могут указывать на важность или мощность объекта, маленькие размеры могут указывать на незначительность или нежелательность.
Пропорции фигуры также могут дать некоторые подсказки о ее сущности. Хорошо пропорционированные фигуры могут указывать на гармонию, ровность или симметрию, тогда как непропорциональные фигуры могут выделяться, привлекая внимание или вызывая необычность.
Расположение фигуры относительно других элементов на плоскости также имеет значение при интерпретации. Близость или удаленность от других объектов может указывать на связи или иерархию, а также на распределение и организацию элементов.
В целом, при анализе фигур в плоской проекции важно учитывать их размеры, пропорции и расположение, чтобы получить более полное представление о их значениях и назначении.
Как прочитать фигуру на поверхности?
Во-первых, необходимо обратить внимание на форму и размеры проекции. Различные фигуры и объекты могут иметь разные проекции на поверхность, что может отражаться в их размерах и пропорциях. Например, проекция куба будет выглядеть как четырехугольник, а шара – как окружность.
Кроме того, можно учитывать и другие детали, такие как линии, узоры или текстуры, которые могут появиться на проекции. Эти элементы могут указывать на наличие дополнительных структур или особенностей в фигуре. Например, появление геометрических линий на проекции может указывать на наличие ребер или граней в фигуре.
В целом, интерпретация фигур в их проекциях на поверхность требует внимательного анализа формы, размеров, ориентации и деталей. Это позволяет лучше понять геометрические объекты и их свойства.
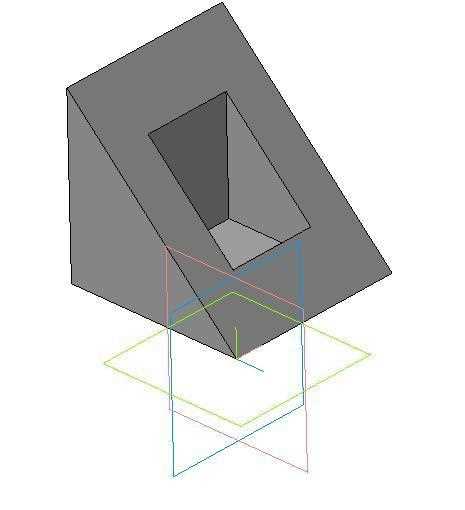
Как интерпретировать фигуры в трехмерной проекции?
Фигуры, представленные в трехмерной проекции, могут быть интерпретированы с помощью анализа их формы, размеров и расположения в пространстве. Когда мы рассматриваем трехмерную проекцию, мы видим объекты в виде двухмерных изображений на плоскости. Важно учитывать, что проекция может искажать исходную форму и размеры объекта, поэтому требуется точность в интерпретации.
Основные приемы интерпретации фигур в трехмерной проекции включают оценку углов, длин сторон, соотношения размеров, симметрии и расположения объектов в пространстве. Углы могут указывать на форму фигуры и ее ориентацию. Длины сторон и соотношения размеров помогают определить пропорции объекта и их соответствие исходным параметрам. Симметрия может отражаться в одинаковых отрезках или параллельных линиях.
- Углы: Оцените углы между линиями и поверхностями, чтобы определить форму и ориентацию объекта. Например, прямоугольник будет иметь прямые углы, а треугольник — углы разной величины.
- Длины сторон и соотношение размеров: Сравните длины отрезков и их соотношение с известными параметрами объекта, чтобы определить пропорции фигуры. Например, соотношение сторон в прямоугольнике должно быть равным.
- Симметрия: Обратите внимание на наличие симметричных элементов или параллельных линий. Они могут указывать на симметричную форму фигуры.
- Расположение: Изучите положение фигуры в пространстве и ее взаимное расположение с другими объектами. Например, куб находится на одной плоскости, в то время как конус расположен выше.
Правильная интерпретация фигур в трехмерной проекции требует внимательного анализа и сравнения с исходными параметрами объекта. Важно учитывать возможные искажения, которые могут возникнуть в процессе проецирования. Отмечая геометрические особенности и понимая их значения, мы можем более точно интерпретировать фигуры в трехмерной проекции.
Короткое описание
Переносим двухмерные фигуры в трехмерное пространство – это важное навык, который помогает понять геометрические объекты в трехмерной проекции. Для этого необходимо анализировать углы, длины и формы фигур, обращать внимание на взаимное расположение элементов. Техника интерпретации трехмерных фигур помогает улучшить визуальную разрядку и способна существенно повысить эффективность работы с пространственными конструкциями.
Вопрос-ответ:
Как интерпретировать фигуры в трехмерной проекции?
Интерпретация фигур в трехмерной проекции включает в себя анализ и понимание формы, размера, положения и ориентации объектов в пространстве.
Какими методами можно интерпретировать фигуры в трехмерной проекции?
Для интерпретации фигур в трехмерной проекции применяются различные методы, такие как изометрическая проекция, косоугольная проекция, изометрическая основа и др.
Что такое изометрическая проекция и как ее интерпретировать?
Изометрическая проекция — это способ представления трехмерного объекта на плоскости таким образом, чтобы все его оси были отображены в одинаковом масштабе и под углом 120 градусов. Интерпретация изометрической проекции включает в себя анализ размеров и форм объектов, а также определение их положения по отношению друг к другу.
Как интерпретировать фигуры в косоугольной проекции?
Косоугольная проекция — это способ представления трехмерных объектов на плоскости с использованием наклоненных проекционных плоскостей. Интерпретация фигур в косоугольной проекции включает в себя анализ формы, размеров и положения объектов, а также определение их ориентации по отношению к проекционным плоскостям.
Что такое изометрическая основа и как ее интерпретировать?
Изометрическая основа — это схематическое представление изометрической проекции, в которой оси объекта представлены в виде пересекающихся линий. Интерпретация изометрической основы включает в себя анализ положения и пространственного расположения объектов на основе их отображения на оси.
Как интерпретировать фигуры в трехмерной проекции?
Для интерпретации фигур в трехмерной проекции необходимо учитывать их положение в пространстве, относительные размеры и взаимное расположение точек. При анализе трехмерных проекций необходимо обращать внимание на масштаб, перспективу, а также использовать знания о геометрии и принципах трехмерного моделирования. Умение визуализировать трехмерные объекты и понимать их пространственные характеристики является важным навыком при работе с трехмерной графикой, архитектурным проектированием, инженерией и другими смежными областями.
Как правильно интерпретировать фигуры в трехмерной проекции?
Для правильной интерпретации фигур в трехмерной проекции необходимо использовать навыки геометрии и трехмерного моделирования. Сначала следует рассмотреть положение и ориентацию фигуры в пространстве, а затем обратить внимание на перспективу и масштаб. Некоторые фигуры в трехмерной проекции могут выглядеть искаженными из-за перспективы, поэтому важно учитывать этот факт при их интерпретации. Также полезно использовать визуализацию или компьютерные программы для более точного представления трехмерных объектов. Практика и опыт помогут улучшить навыки интерпретации трехмерных фигур.